Que recherchez-vous ?

» BATONS POUR CALCULER

BATONS POUR CALCULER

Revenir à l'accueil

Retrouver nos bâtons pour calculer : ici

METHODE - BATONS POUR CALCULER

Voici une méthode fabuleuse pour apprendre et s'initier aux chiffres et aux mathémétiques de façon ludique avec de simples bâtons.

De l'approche des chiffres aux divisions et aux puissances, ces bâtons accompagneront votre enfant pendant de nombreuses années.

3 moyens d'appréhension :

Dans un premier temps, votre enfant va assimiler les réglettes, et les nombres qu'elles représentent, en observant leur longueur et leur couleur. La mémoire visuelle, la mémoire auditive, et la mémoire tactile interviennent, pour chaque enfant suivant sa meilleure sensibilité. La mise en action de ces trois types de mémoire active ces différentes facultés, accélère le processus d'apprentissage, et compense l'une ou l'autre déficience de perception.

L'auto-correction :

A chaque stade de l'apprentissage, votre enfant aura l'occasion de s'auto-corriger, et de comprendre pourquoi sa réponse est correcte ou incorrecte. C'est une puissance incontestable de la méthode CUISENAIRE qui remplacera la sanction du maître ou la "correction radicale du bic rouge"

Les différentes phases de l'apprentissage :

1- PHASE QUALITATIVE

D'abord, la familiarisation avec les réglettes.

Chaque réglette est personnalisée, dans une boîte pêle-mêle par:

sa couleur
sa longueur
ses relations avec les autres

Une réglette ne représente un nombre que en relation avec les autres réglettes.

La rouge est plus grande que la blanche, et plus petite que la verte... Etc
toutes les jaunes ont la même longueur...

JEUX :

construire des trains / comparer 2 trains

construire des tapis

construire des escaliers

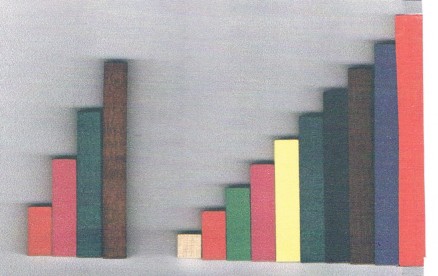
reconnaitre les réglettes les yeux fermés

(par exemple en prenant une poignée de réglettes derrière le dos)

construire des silhouettes symétriques ou pas.

A l'école maternelle, et en tout cas en début d'apprentissage, il faut éviter d'associer un nombre sur la réglette, afin que les notions de plus grand, plus petit, double, demi, égal, etc ... aussi bien que devant, derrière, au-dessus, en-dessous, à côté de, symétrique, parallèle, perpendiculaire... soient bien maîtrisées.

2- PHASE QUANTITATIVE

On commence par construire un escalier 1,2,3,4,5,6,7,8,9,10

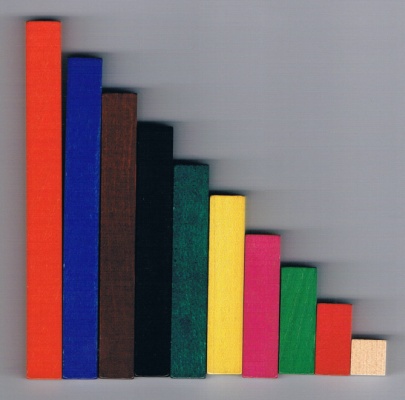
Et on le nomme : 1,2,3,4,5,6,7,8,9,10.

Toute contestation peut être vérifiée, en alignant des réglettes 1 le long de la réglette inconnue.

On est alors entré dans le système décimal et on va commencer à calculer

On vérifie d’abord que l’enfant maîtrise que dans le système décimal, le nombre correspond directement à une couleur et à une longueur :

Dans un tas de réglettes pêle-mêle, sélectionner tous les 5…, toutes les bleues… etc
Même chose à l’aveugle, avec une poignée dans le dos, sélectionner la réglette 5…, sélectionner la réglette rouge… etc

JEUX :

Organiser des jeux avec deux concurrents : celui qui trouvera le plus de 5…, celui qui trouvera le plus vite…

Ensuite, on situe le nombre dans la suite des nombres :

5 est plus grand que 4 et plus petit que 6
on vérifie ensuite sur l’escalier
on vérifie que le 5 vaut bien 5 réglettes 1
on fait le même exercice de mémoire, sans les réglettes (5 est plus grand que 4, et plus petit que 7, et que 6…)
on vérifie à nouveau avec les réglettes que la réponse est correcte

3- L'ADDITION

on compose d’abord des tapis. Par exemple de longueur 8

Avec deux réglettes
Avec plus de deux réglettes
Avec des réglettes semblables

Avec deux réglettes

On remarque que, après la pose de la première réglette, il y a un tâtonnement pour trouver la bonne deuxième réglette pour le tapis de longueur 8

chaque enfant construit le tapis qui lui plaît ( pas de copie ni de plagiat)
il y a une autocorrection (didactiquement positif)
la correction est immédiate (rapide)

lorsque le tapis est composé, l’enfant lit ( à haute voix) ce qu’il a composé :

8, c’est 7+1, c’est 3+5, ….

ensuite, il écrit ce qu’il a composé.

ensuite, on retire la réglette de droite, en maintenant le reste du tapis.

ensuite, l’enfant écrit en regardant le tapis décomposé tous les trains du tapis du nombre 8, mais sans manipuler les réglettes . 8, c’est 7+(1) ? c’est 3+(5) ? ….

ensuite, l’enfant vérifie que ce qu’il a écrit est correct en ajoutant les réglettes manquantes. (c’est une autocorrection rapide)

L’enfant a écrit 3+6, il voit que ceci dépasse le tapis de 8. Il voit que le 6 est trop grand; il prend une plus petite; en tâtonnant, il voit que la bonne solution est 3+5.

Avec plus de deux réglettes

même exercice
faire remarquer à l’enfant qu’il peut grouper plusieurs réglettes
faire remarquer à l’enfant qu’il peut permuter plusieurs réglettes sans affecter le résultat.

Avec des réglettes semblables

même exercice
remarquer que toutes les compositions ne sont pas possibles
à conserver pour plus tard pour introduire la multiplication

Tous ces exercices et jeux doivent être repris avec d’autres nombres. D’abord, pour les 20 ou 30 premiers nombres (suivant les seuils de compétence demandés), et ensuite, les 100 premiers nombres. Il est important que l’enfant y découvre que les réponses sont chaque fois différentes, mais que les procédés pour y arriver sont toujours les mêmes.

4- LA SOUSTRACTION

L’approche de la soustraction peut se faire de la même manière que l’addition, à l’aide des tapis.

sur le tapis de 8, inviter l’enfant à retirer 1, il reste 7.
si on retire 1 à 8 il reste 7
l’enfant écrit 8 – 1 = 7

Même exercice – autre représentation :

On peut aussi exprimer la soustraction en posant la deuxième réglette sur la première :

l’enfant peut vérifier de la même manière si sa réponse est exacte :

il pose la réglette 5 sur la réglette 8, et il dit 8 – 5 = ?

S’il dit 4? il prend la réglette 4, et il la pose sur le 8; c’est trop grand, il tâtonne, il trouve finalement 3, et comprend que 8 – 5 =3

plus tard, on introduit ainsi les nombres négatifs :

si on retire 5 à la réglette 8, il reste 3…
si on retire 10 à la réglette 8

Le 10 dépasse de 2 , et on dit 8 – 10 = (-2)

Cette manipulation peut aussi se faire en utilisant la règle de calcul.

Les mêmes exercices sont à reproduire pour les 100 premiers nombres afin que l’enfant observe que les résultats sont chaque fois différents , mais les procédés sont les mêmes.

5- LA MULTIPLICATION

reprendre l’exercice proposé pour l’addition, par exemple pour le nombre 12
inviter l’enfant à composer un tapis de 12 uniquement avec des réglettes semblables
il observe qu’il peut réaliser 12 avec certains trains :
- 6 + 6
- 3 + 3 + 3 + 3
- 2 + 2 + 2 + 2 + 2 + 2
- 4 + 4 + 4

Mais pas avec tous: avec 5, avec 7, avec 8, avec 9, il n’arrive pas à réaliser le tapis de 12.

il remarque aussi que pour certains nombres ( 13 par exemple) il peut essayer toutes les combinaisons, mais aucune n’est exacte (sauf avec la réglette 1) – (ce sont les nombres premiers)
concentrons-nous maintenant sur le tapis de 12 pour lequel il y a plusieurs trains

Au lieu de dire

6 + 6, l’enfant dira 2 x 6
2 + 2 + 2 + 2 + 2 + 2, l’enfant dira 6 x 2
4 + 4 + 4, l’enfant dira 3 x 4
3 + 3 + 3 + 3, l’enfant dira 4 x 3

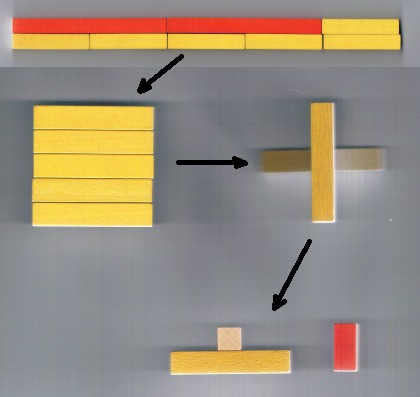
Au lieu de représenter 12 par un train, il peut aussi le représenter par un rectangle. Inviter l’enfant à faire cette manipulation en pinçant les deux réglettes 6 entre 2 doigts. 2 x 6, c’est 2 réglettes 6, c’est un rectangle dont 1 côté fait 6 et l’autre côté fait 2

De même, avec les rectangles 6 x 2, 3 x 4, 4 x 3. L’enfant peut aussi mesurer les dimensions du rectangle avec une autre réglette.

Inviter l’enfant à prendre maintenant le rectangle de 6 x 2 et à le poser sur le rectangle 2 x 6. Il observe qu’ils sont les mêmes (commutativité de la multiplication)

montrer alors à l’enfant qu’il peut aussi représenter le nombre 12 avec moins de réglettes (uniquement les deux côtés du rectangle) et former le produit en croix 6 x 2 ou 2 x 6.

l’enfant peut faire la même manipulation avec les autres trains de 12. 4 x 3 et 3 x 4 , et représenter 12 par son produit en croix :

le même exercice est applicable à tous les nombres. Les nombres qui ont des diviseurs peuvent tous être représentés par un produit en croix.

JEUX :

deux adversaires ne représentent les nombres que par leurs produits en croix. Le premier compose, le second (ou plusieurs autres) devinent le nombre représenté…
l’exercice peut être compliqué en représentant les nombres par des «tours» plus hautes. Dans l’exemple ci-dessus, le nombre 12 peut encore être représenté par 2 x 2 x 3 (c’est une tour de hauteur 3)
le jeu ci-dessus peut être répété avec des tours plus hautes.
autre jeu: inviter l’enfant à réaliser la tour la plus élevée possible. Elle est composée des réglettes les plus petites (il a aussi décomposé le nombre en facteurs premiers – utile pour l’introduction du ppcm et du pgcd)

Ceci est un bon exercice pour l’apprentissage des tables de multiplication. Le jeu peut être organisé, soit avec les produits en croix complets, soit en subtilisant une réglette, soit sans réglette et en vérifiant les résultats contestés lors du jeu.

6- LA DIVISION

Lorsque l’enfant maîtrise bien la représentation des nombres en croix, il est prêt pour aborder la division.

sur le tapis de 12, il observe

Si 12, c’est 2 x 6, 6, c’est la moitié de 12
De même... 4 est le tiers de 12
...3 est le quart de 12, etc...

sur la représentation en croix, faire remarquer à l’enfant que, pour connaître la moitié, il prend la réglette 2, et il lui reste la réponse: 6

De même, pour trouver le tiers de 12, il prend la réglette 3 et la réponse est 4. Etc…

JEUX :

plusieurs enfants confectionnent des produits en croix.
l’un demande aux autres de lui donner le tiers de…, le quart de…

Jeu plus difficile

Sans avoir les produits en croix devant les yeux.

Jeu supplémentaire

Effectuer des additions, des soustractions, multiplications de fractions.

A chaque fois, ou à chaque contestation, les enfants peuvent vérifier en recomposant le produit en croix, ou encore, en recomposant les trains du tapis.

Les buts atteints sont: autocontrôle, maîtrise des fractions, rapidité de calcul.

7- LES PUISSANCES

Lors de l’étude de la multiplication, l’enfant construit les tapis avec des réglettes semblables, et de là, a trouvé une nouvelle représentation d’un nombre par deux réglettes mises en croix.

Parmi les nombres étudiés , certains ont la particularité d’être représentés en croix poar deux réglettes semblables . C’est le cas de :